Comment l'avion vole-t-il ?

1. Qu'est ce que le principe de Bernoulli ?

D.Bernoulli (1700-1782) est un mathématicien, physicien et médecin suisse. Ami de Leonard Euler, il travailla sur de nombreux problèmes scientifiques tel que la théorie de l'élasticité, le mécanisme des marées mais aussi économique avec son Paradoxe de Saint Pétesbourg ou encore astronomique. Néanmoins, il est surtout connu pour un principe qui porte son nom, posant les bases de la mécanique des fluides.

Ce théorème établit que : " si un liquide non visqueux, de masse volumique constante ρ, s'écoule en régime permanent dans un tuyau épousant les formes d'une veine de courant, il n'existe pas de remous; les seules forces intervenant étant la force de pesanteur et les forces présentes à l'amont et à l'aval "

On considère l'écoulement permanent ( c'est à dire sans aller-retour ) d' un fluide parfait ( qui n'est pas soumis aux forces de frottement ) entre les sections S₁ et S₂ d'un tuyau d'altitude respective z₁et z₂. Soit m, la masse et V, le volume du fluide qui passe de la section S₁à la section S₂ entre les instants t et t+Δt. Tout se déroule comme si ce fluide était passé de la position (1) à la position (2).

On applique alors le théorème de l'énergie cinétique : " La variation de l'énergie cinétique pour un solide ponctuel de masse m constante dans un référentiel galiléen, parcourant un chemin entre les points A et B est égale à la somme des travaux des forces ( $\overrightarrow{F}$ ) appliqués au solide lors du déplacement. "

avec :

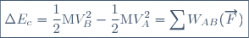
- $\Delta E_c$ : Variation de l'énergie cinétique entre la position 2 et la position 1 (J)

- M : La masse du soilde (kg)

- V : La vitesse du solide (m.s^-1)

- $\sum W_{AB}(\overrightarrow{F})$ : La somme des travaux des forces appliquées au solide (J)

C'est à dire que la variation de l'énergie cinétique est égale à la somme des variations des forces extérieurs : le poids et les forces exercées en amont et en aval.

De plus l'énergie contenue dans un fluide en mouvement se retrouve sous deux formes : l'énergie cinétique ( celle due à sa vitesse ), l'énergie potentielle ( due à la pression ).

Le théorème de Bernoulli s'exprime sous la forme d'une équation de conservation de l'énergie mécanique du fluide, après simplification :

1/2(ρ*v²) + ρgz + p = constante

avec :

- ρ : masse volumique ( kg/m³)

- v : vitesse ( m.s^-1)

- p : pression ( Pa )

- g : accélération de la pesanteur ( N.kg^-1)

- z : altitude (m)

où, 1/2(ρ*v²) est l'énergie cinétique de l'unité de volume et ρgz + p est son énergie potentielle (ou pression de pesanteur)

Grâce à cette équation, on en déduit que lorsque un facteur augmente, un autre facteur de l'équation doit diminuer pour garder la constante. Ainsi, si la vitesse augmente, la pression baisse et inversement.

2. Qu'est ce que l'effet Venturi ?

Le théorème de Bernoulli permet de nombreuses applications pratiques et notamment l'effet Venturi. Du nom de Giovanni Baptista Venturi ( 1746 - 1822 ), prêtre et physicien italien, ayant aussi travaillé sur l'acoustique et l'optique.

On se place toujours dans le cas d'un fluide parfait incompressible et s'écoulant de manière permanente et sans frottement. Soit m, la masse et V, le volume du fluide. Le tube est composé de 3 parties, une ayant un diametre largement inférieur au 2 autres et se situant au milieu. Dans la partie 1 de la canalisation, le fluide s'écoule à une vitesse v₁ et dans la partie 2 à une vitesse v₂. 2 tubes latéraux, Ps₁ et Ps₂, se situant sur la partie 1 et la partie 2, permettent la prise de pressions.

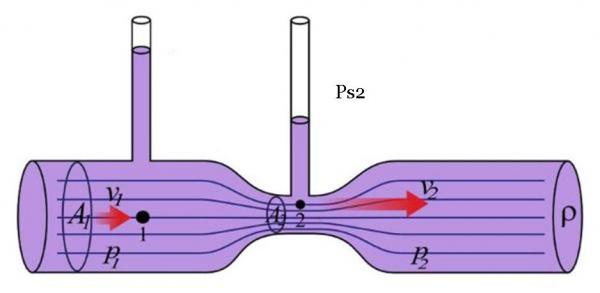
Le fluide étant en régime permanent, le débit est constant. Ainsi : Q₁ = A₁.v₁ = Q₂ = A₂.v₂

d'où, v₂ = v₁ * (A₁/A₂) > v₁

La relation de Bernoulli s’écrit sous la forme :

1/2(ρ*v₂²) +Ps_{2 =} 1/2(ρ*v₁²) + Ps_1, avec Ps₁ et Ps₂, la pression de pesanteur

d’où:

Ps_{1 -}Ps_{2 = 1/2}ρ( v₂²- v₁²) > 0

Donc : Ps₂ < Ps₁. Ainsi, lorsque que la canalisation se rétrécit, le fluide accélère et la pression diminue. Il en va de même à l'inverse, quand la canalisation s'agrandit, le fluide décèlère et la pression augmente. Ce résultat est assez peu intuitif, en effet on s'attend a voir la pression augmenter quand la section du tuyau diminue.

3. Les ailes de l'avion lui servent-elles à glisser sur l'air ?

Non, les ailes d'un avion ne fonctionnent pas sur l'air comme un surf sur la mer ou des skis sur la neige.

Pour comprendre leur utilité, nous prendrons l'exemple d'un avion léger ne comprenant qu'un seul moteur, comme ceux utilisé pour passer le brevet de pilote. Celui-ci volera en palier, c'est à dire de manière parfaitement rectiligne, à une vitesse constante et sans variation d'altitude. Tout cela dans le but de faciliter les calculs et la compréhension du phénomène.

Tout d'abord, il faut savoir que l'avion est dans une situation d'équilibre : les 4 forces qui agissent sur lui s'annulent ( pratiquement car sinon l'avion ferait du surplace). Ces 4 forces, exprimées en Newton (N), sont le poids P, la traction T, la portance Rz et la trainée Rx. Les 2 premières sont la décomposition de la résultante mécanique et les 2 suivantes sont la décomposition de la résultante aérodynamique.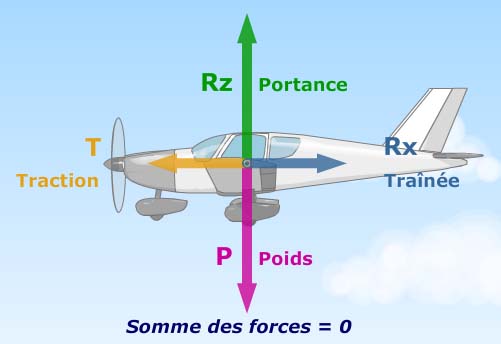

Elles sont liées au mouvement relatif de l'avion vis à vis de l'air, déplacement de l'avion et celui de l'air vis à vis de l'avion, le vent : les mouvements mis en jeu sont identiques dans les 2 cas et sont appellés vent relatif.

Le poids est le plus sérieux handicap de l'avion, c'est le résultat de la force de gravitation qui s'exerce sur Terre. Il s'applique au centre de gravité de l'avion et est donné par la formule:

P = m.g

avec :

m, la masse (kg)

et g, la constante gravitationnelle (N.kg)

Autrefois, on pensait que les objets étaient plus lourds que l'air ne pouraient jamais voler. C'était sans compter une autre force : la portance

La portance compense le poids et explique la conception même des ailes d'avions, sans lesquelles un plus lourd que l'air ne pouvait voler. Celles-ci sont légèrement bombées sur le dessus ( voir dessin ), l'extrados. De plus, l'aile n'est pas parallèle au sol, elle forme avec l'horizontale un angle, l'angle d'incidence. Ainsi, le vent relatif, qui contourne l'aile par l'extrados, doit se " presser "entre le bord supérieur de l'aile et les couches d'air situées au-dessus d'elle et qui ne sont pas perturbées par le passage de l'avion. C'est comme si l'air devait passer dans un tube plus étroit, donc , d'après l'effet Venturi, l'air accélère. Et il se créée une dépression sur l'extrados de l'aile : celle-ci est aspirée vers le haut.

Il se passe plus ou moins la même chose sur l'intrados de l'aile, sauf que le vent relatif doit freiner très fortement à cause de l'obstacle qu'amène l'angle d'incidence. Et de nouveau d'après Venturi et Bernoulli, l'air décélère et il se crée une supression : l'aile est alors poussée vers le haut. C'est l'addition de ces 2 effets qui donne la portance, on estime que la dépresion au dessus de l'aile contribue à 2/3 de la portance, alors que la surpression en dessous de l'aile, y participe au 1/3.

La portance est perpendiculaire au vent relatif et s'exerce sur le centre de poussée de l'avion. Elle se calcule par la formule :

Rz = 1/2.ρ.C_z.V².S

avec :

ρ, la masse volumique de l'air qui varie en fonction de l'altitude ( kg/m² )

C_z, le coefficient de portance de l'aile, il dépend du profil de l'aile et de l'angle d'incidence

V, la vitesse d'écoulement de l'air ( m.s^-1 )

et S, la surface de l'aile ( m² )

La portance vient ainsi compenser le poids ( voir 4. ), mais elle ne s'exerce qu'à partir d'une certaine vitesse, voila l'explication de la brusque accélération exercée lors du décollage pour atteindre cette vitesse.

Le vol d'un avion coincide donc à un juste équilibre entre le poids et la portance, le tout fluctuant grâce à la vitesse. Ainsi lors du décollage, la portance est supérieure au poids, puis durant le vol, ils s'équilibrent pour s'inverser durant la phase d'atterissage.

Le vent relatif est aussi responsable d'une autre force : la trainée

C'est la résistance de l'air au mouvement de l'avion, ainsi plus l'avion va vite, plus la trainée est importante. Elle est parallèle au vent relatif et s'exerce sur le centre de poussée. Elle se calcule par la formule :

Rx = 1/2ρ.C_x.V².S

avec : C_x, le coefficient de trainée, il dépend de la forme de l'aile et de l'angle d'incidence

A la trainée s'oppose la force de traction. Elle est fournie par le moteur et est dans l'axe de ceux-ci. La force exercée par le moteur est légèrement supérieure à celle exercée par la trainée : en effet, si elles étaient égales, l'avion ferait du surplace.

4. Qu'est ce que la 3eme loi de Newton ?

Newton (1643-1727) est un physicien anglais qui a enseigné au Trinity Collège de Cambridge. Dans son ouvrage "Philosophiae naturalis principia mathematica", paru en 1687, il énonce la loi de la gravitation universelle et les trois lois universelles du mouvement, principes à la base de la mécanique classique. La 1^ère loi porte sur le principe d'inertie et la 2^nde sur le principe fondamental de la dynamique de translation.

La 3eme loi de Newton, ou principe des actions réciproques est exprimé de la manière suivante: " Tout corps A, exerçant une force sur un corps B, subit une force d'intensité égale, de même direction mais de sens opposée, exercée par le corps B". C'est à dire que 2 corps exercent toujours l'un sur l'autre des actions égales mais dirigés en sens opposés. Physiquement parlant, cela donne: F_A/B= - F_B/Amais aussi F_A/B+ F_B/A= 0.

Application à l’avion : Le vent est dévié vers le bas, au bord de fuite de l'aile. Il subit une force (D) de la part de l’aile ; donc celle-ci a subi une force (P) en retour d’après la 3^e loi de Newton. Ainsi (D) et (P) sont opposées. Or (D) est verticale et dirigée vers le bas, donc (P) est verticale et dirigée vers le haut. Toujours d’après la 3^e loi de Newton, │P│=│D│ d’où la valeur de (P) est proportionnelle au volume d’air déplacé sous l’action de l’aile. (P) s’appelle la portance.